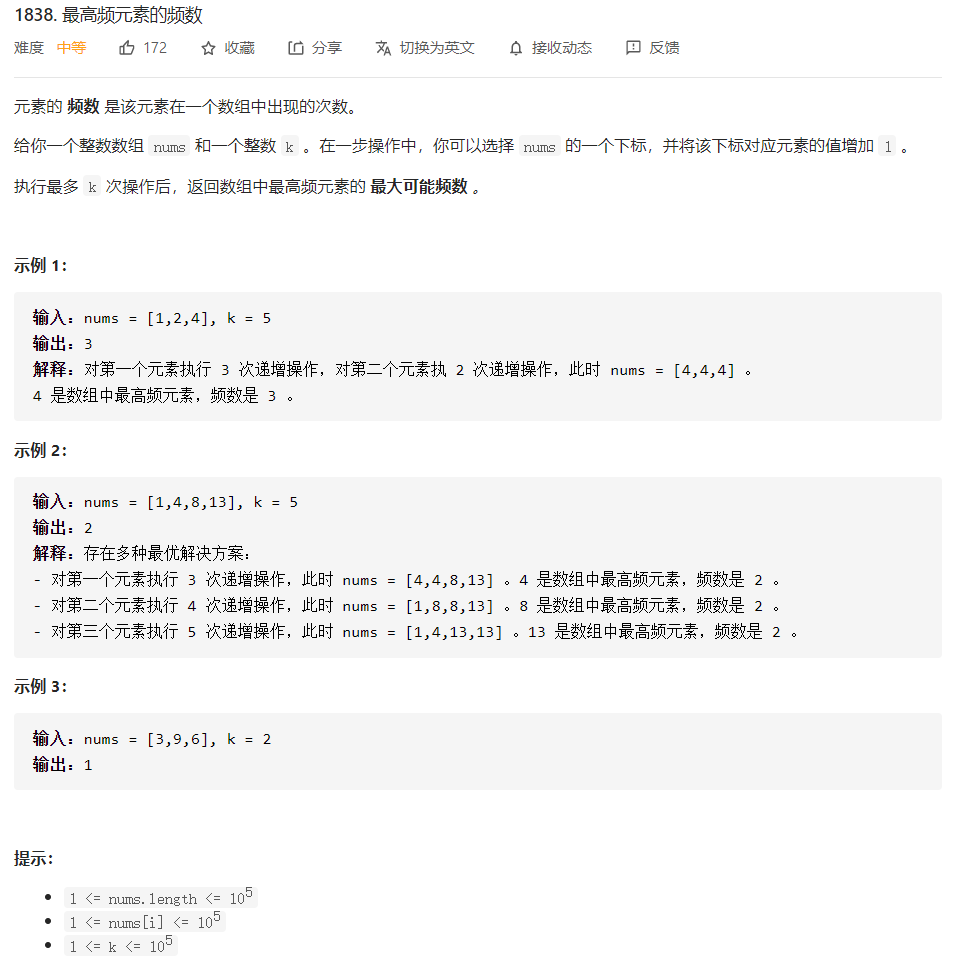
题目分析

一开始做这个题目的时候，使用暴力法进行求解，先进行排序，再以每一个数为基准，并将小于该元素的数加至该元素，当加k个值时停止。这种方法时间复杂都为O(nk)，因为n和k都是1e5的数据，因此无法通过所有样例。小伙伴们能否找到更好的算法呢？

滑动窗口

我们寻找时间复杂都较大的原因，我们对于从低到高的所有元素都计算了差值，举一个例子nums = [1,2,3,4,5,6] , k = 4，使用分析中的方法时
以1为上界，后面没有元素，因此频数为1
以2为上界，后面只有1，而且2 - 1 = 1，可以将1变为2，因此频数为2
以3为上界，后面有2和1，而且3 - 2 = 1，3 - 1 = 2，将2和1都变为3，因此频数为3
以4为上界，后面有3，2和1，而且4 - 3 = 1，4 - 2 = 2，4 - 1 = 3 将3和2都变为4，因此频数为3
后面同理，可以发现一个问题，下标为i的数到后面的距离之和等于下标为i - 1的数到后面的距离之和 + (nums[i] - nums[i + 1]) * i。这个规律很好理解，后面的数不但要补齐与第i - 1个元素的差距，还要额外补齐到第i个元素的差距。因此就可以省去遍历后面元素的计算过程。

算法的时间复杂度为$O(nlog(n))$，空间复杂度为$O(1)$

下面是Java语言的题解

class Solution {
    public int maxFrequency(int[] nums, int k) {
        Arrays.sort(nums);
        int left = 0;
        int right = 1;
        long cur = 0;
        int res = 1;
        while (right < nums.length) {
            while (right < nums.length && cur + (right - left) * (nums[right] - nums[right - 1]) <= k) {
                cur += (right - left) * (nums[right] - nums[right++ - 1]);
            }
            res = Math.max(res, right - left);
            cur -= nums[right - 1] - nums[left++];
        }
        return res;
    }
}

刷题总结

本题是一个非常有趣的滑动窗口题目，小伙伴们没有思路时可以从暴力法中获得灵感。